Hipérbola
Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.
Ecuaciones de la hipérbola
Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas 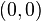 y ecuación de la hipérbola en su forma canónica.
y ecuación de la hipérbola en su forma canónica.
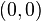 y ecuación de la hipérbola en su forma canónica.
y ecuación de la hipérbola en su forma canónica.
Ecuación de una hipérbola con centro en el punto 

Ejemplos:
a)
b)
Si el eje x es positivo, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.
Tomado de: http://es.wikipedia.org/wiki/Hip%C3%A9rbola



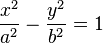
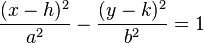


No hay comentarios:
Publicar un comentario