Exponentes y Radicales

Los exponentes también se llaman potencias o índices

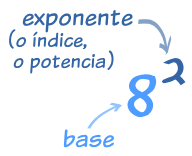El exponente de un número nos dice cuántas veces se usa el número en una multiplicación. En este ejemplo: 82 = 8 × 8 = 64 En palabras: 82 se puede leer "8 a la segunda potencia", "8 a la potencia 2" o simplemente "8 al cuadrado"

Más ejemplos:

Ejemplo: 5³ = 5 × 5 × 5 = 125

• En palabras: 5³ se puede leer "5 a la tercera potencia", "5 a la potencia 3" o simplemente "5 al cubo"

Ejemplo: 2⁴ = 2 × 2 × 2 × 2 = 16

• En palabras: 2⁴ se puede leer "2 a la cuarta potencia" or "2 a la potencia 4" o simplemente "2 a la cuarta"

Y los exponentes hacen más fácil escribir muchas multiplicaciones

Ejemplo: 9⁶ es más fácil de escribir y leer que 9 × 9 × 9 × 9 × 9 × 9

Puedes multiplicar cualquier número por sí mismo tantas veces como quieras con esta notación.

Así que, en general:

an te dice que multipliques a por sí mismo, y hay n de esos a's:

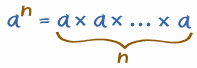Exponentes negativos

¿Negativos? ¿Qué es lo contrario de multiplicar? ¡Dividir! Un exponente negativo significa cuántas veces se divide entre el número.

Ejemplo: 8^-1 = 1 ÷ 8 = 0,125

O varias divisiones:

Ejemplo: 5^-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0,008

Pero esto lo podemos hacer más fácilmente:

5^-3 también se podría calcular así:

1 ÷ (5 × 5 × 5) = 1/5³ = 1/125 = 0,008

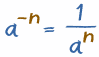Este último ejemplo nos muestra una manera más fácil de manejar exponentes negativos: Calcula la potencia positiva (an) Después cacula el recíproco (o sea 1/an)

Más ejemplos:

Exponente negativo		Recíproco del exponente positivo		Respuesta
4-2	=	1 / 42	=	1/16 = 0,0625
10-3	=	1 / 103	=	1/1.000 = 0,001

¿Qué pasa si el exponente es 1 o 0?

Si el exponente es 1, entonces tienes el número solo (por ejemplo 9¹ = 9)
Si el exponente es 0, la respuesta es 1 (por ejemplo 9⁰ = 1)

Tiene sentido

Mi método favorito es empezar con "1" y multiplicar y o dividir tantas veces como diga el exponente, y tendrás la respuesta correcta, por ejemplo:

Ejemplo: potencias de 5
	... etc...
52	1 × 5 × 5	25
51	1 × 5	5
50	1	1
5-1	1 ÷ 5	0,2
5-2	1 ÷ 5 ÷ 5	0,04
	... etc...

Si miras esta tabla, verás que los exponentes positivos, cero y negativos son en realidad parte de un mismo (y bastante sencillo) patrón.

Leyes de los Exponentes

La ley que dice que x^mxⁿ = x^m+n

En x^mxⁿ, ¿cuántas veces multiplicas "x"? Respuesta: primero "m" veces, despuésotras "n" veces, en total "m+n" veces.

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

Así que x²x³ = x⁽²⁺³⁾ = x⁵

La ley que dice que x^m/xⁿ = x^m-n

Como en el ejemplo anterior, ¿cuántas veces multiplicas "x"? Respuesta: "m" veces, después reduce eso "n" veces (porque estás dividiendo), en total "m-n" veces.

Ejemplo: x^4-2 = x⁴/x² = (xxxx) / (xx) = xx = x²

(Recuerda que x/x = 1, así que cada vez que hay una x "sobre la línea" y una "bajo la línea" puedes cancelarlas.)

Esta ley también te muestra por qué x⁰=1 :

Ejemplo: x²/x² = x^2-2 = x⁰ =1

La ley que dice que (x^m)ⁿ = x^mn

Primero multiplicas x "m" veces. Después tienes que hacer eso "n" veces, en total m×n veces.

Ejemplo: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

Así que (x³)⁴ = x^3×4 = x¹²

La ley que dice que (xy)ⁿ = xⁿyⁿ

Para ver cómo funciona, sólo piensa en ordenar las "x"s y las "y"s como en este ejemplo:

Ejemplo: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

La ley que dice que (x/y)ⁿ = xⁿ/yⁿ

Parecido al ejemplo anterior, sólo ordena las "x"s y las "y"s

Ejemplo: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

La ley que dice que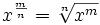

Para entenderlo, sólo recuerda de las fracciones que n/m = n × (1/m):

Ejemplo:

Bibliografía:

http://www.disfrutalasmatematicas.com/exponentes.html